实验32 圆柱壳静力分析
一、实验课题
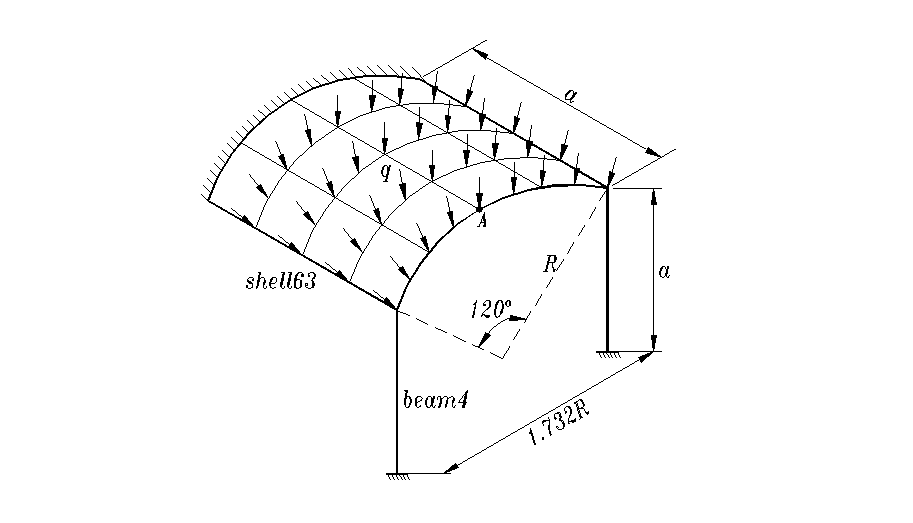
圆柱壳半径R = 4 m,长a = 8 m,厚t = 0.2 m,承受均布法向载荷q = 1 MPa,壳的一条边固定,另一条边由两根直径d = 0.2 m的梁支撑。已知材料的弹性模量 E = 20 GPa,泊松比μ= 0.3,试用ANSYS对此圆柱壳静力分析。
二、实验要求
1 掌握圆柱坐标系的运用
;
2 掌握圆柱壳的生成方法
;
3 掌握单元网格疏密的控制方法
;
4 掌握面载荷的定义方法
。
三、ANSYS操作步骤:
Ⅰ 建立有限元模型
1 输入标题
(1) 点击【File】→【Change Title】;
(2) 输入标题“薄板弯曲问题静力分析 1”;
(3) 点击【OK】按钮。
2 选择分析类型
(1) 点击【Main Menu】→【Preferences】;
(2) 选择 structural 复选框,然后点击【OK】按钮。
3 确定单元类型
(1) 点击【Main Menu】→【Preprocessor】→【Element Type】→【Add/Edit/Delete】→【Add】;
(2) 选择 structural Shell 族中 Elastic 4node 63 单元,点击【Apply 】;
(3) 再选 structural Beam 族中 3D elastic 4 单元,点击【OK 】;
(4) 再击【Close】关闭对话框。
4 定义实常数(截面积)
(1) 点击【Main Menu】→【Preprocessor】→【Real Constants】;
(2) 先点击【Add】,选择 Shell 63,再点击【OK 】;
(3) 输入实常数号 1,厚度 0.2 ,点击【OK】;
(4) 再点击【Add】,选择 Beam4,再点击【OK 】;
(5) 输入实常数号 2 ,截面积 3.1416E-2,对Z惯性矩 0.7854E-4,对Y惯性矩 0.7854E-4,梁Z方向高 0.2,梁Y方向高 0.2,对X惯性矩 1.5708E-4,再点击【OK】和 【Close】。
5 定义材料性质
(1) 点击【Main Menu】→【Preprocessor】→【Material Props】→【Constant-Isotropic】;
(2) 点击【OK】;
(3) 输入弹性模量 20E+9,泊松比 0.3,然后点击【OK】。
6 建立模型
(1) 点击【WorkPlane】→【Change Active CS to】→【Global Cylindrical】;
(2) 点击【Main Menu】→【Preprocessor】→【Modeling Create】→【Keypoints】→【In Active CS】;
输入关键点号 1 ,及其坐标 4 , 30 , 8 ,然后点击【Apply】;
输入关键点号 2 ,及其坐标 4 , 150 , 8 ,然后点击【Apply】;
输入关键点号 3 ,及其坐标 4 , 150 , 0 ,然后点击【Apply】;
输入关键点号 4 ,及其坐标 4 , 30 , 0 ,然后点击【OK】。
(3) 点击【PlotCtrls】→【Pan,Zoom,Rotate】→【Obliq】;
(4) 点击【Main Menu】→【Preprocessor】→【Modeling Create】→【Areas Arbitrary】→【Through KPs】;
依次拾取关键点 1,2,3,4,然后点击【OK】;
(5) 点击【Main Menu】→【Preprocessor】→【Meshing-Size Cntrls】→【ManualSize-Global size】,在框 Element edge length 内输入 0.5 ,然后点击【OK】;
(6) 点击【Main Menu】→【Preprocessor】→【Meshing-Mesh】→【Areas-Free】;
在 Mesh Areas 框点击 Pick All;
(7) 点击【WorkPlane】→【Change Active CS to】→【Global Cartesian】;
(8) 点击【Main Menu】→【Preprocessor】→【Modeling Create】→【Nodes】→【In Active CS】;
输入节点号 201 ,及其坐标 3.4641 , -6 , 8 ,然后点击【Apply】;
输入节点号 202 ,及其坐标 -3.4641 , -6 , 8 ,然后点击【OK】。
(9) 点击【Main Menu】→【Preprocessor】→【Modeling-Create】→【Elements】→【Elem Attributes】,在TYPE 框选 2,REAL 框选 2 ,然后点击【OK】;
(10) 点击【PlotCtrls】→【Numbering】,打开 Node number 复选框,然后点击【OK】;
(11) 点击【Plot】→【Nodes】;
(12) 点击【Main Menu】→【Preprocessor】→【Modeling-Create】→【Elements】→【Auto Numbered-Thru Nodes】;
点取节点 201 ,1 和 202 ,然后点击【Apply】;
点取节点 202 ,2 和 201 ,然后点击【OK】;
(13) 点击【Plot】→【Element】。
Ⅱ 求解
1 定义约束
(1) 点击【Main Menu】→【Solution】→【Loads-Apply】→【Structural-Displacement】→【On Nodes】;
拾取节点 201 ,202 及圆柱壳的一条圆弧边上的所有节点,拾取窗中点击【OK】,
再选择 All DOF ,然后点击【OK】。
2 施加载荷
(1) 点击【Main Menu】→【Solution】→【Loads-Apply】→【Structural- Pressure】→【On Areas】,在 Apply PRES on Areas 框点击 Pick All;
在 Pressure value 框中输入载荷值 1E6 然后点击【OK】。
3 求解
(1) 点击【Main Menu】→【Solution】→【Solve】→【Current LS】;
(2) 浏览完显示的信息后,关闭文本窗口;
(3) 点击【OK】后开始求解;
(4) 点击【Close】。
Ⅲ 后处理
1 画应力云图
(1) 点击【Main Menu】→【General Postproc】→【Plot Results】→【Contour plot-Nodel Solu】;
(2) 选择 Stress 族中 Von Mises 等效应力,然后点击【OK】。
Ⅴ 退出 ANSYS
点击工具栏上【Quit】按钮,选择 quit - no save! 复选框,再点击【OK】。

