题 目：Flow stability in viscoelastic pipe flows
报告人：Dr. Mengqi Zhang (National University of Singapore)
时间：2021年6月2日（周三）下午1:30
地点：上海市静安区延长路149号力学所200会议室
摘要Recent studies indicate that viscoelastic (polymeric) pipe flows can be linearly unstable, in contrast to the linearly stable Newtonian pipe flows. This linear instability mechanism is surprising and has stimulated new interests to further study the flow instability in viscoelastic pipe flows. In this talk, I will first present the state of the art of the research and then introduce our recent works.
The linear instability was found using a relatively simple constitutive model for the polymers, i.e., Oldroyd-B model. A more realistic model, FENE-P model, will be examined in this work and the transient energy growth of the linear modes will be depicted. It is found that an Orr mechanism (along with the critical-layer mechanism) is at play in the conformation tensor field, contributing to the total energy growth.
From a nonlinear point of view, the linear instability implies a possibility of supercritical bifurcation in viscoelastic pipe flows, again, in contrast to the subcritical Newtonian pipe flows. We applied a multiple-scale expansion method to study the bifurcation type in the viscoelastic pipe flows. It is found that the two bifurcation types both exist in this flow and a boundary between them is dictated by the polymer concentration (or viscosity ratio
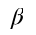). Our theoretical prediction of the bifurcation boundary in
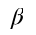is about 0.785(below which, the flow is supercritical; vice versa), which is qualitatively close to the experimental observation
.
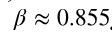Bio: Dr. Mengqi Zhang is an assistant professor in the Department of Mechanics Engineering, National University of Singapore since 2018. He received his PhD in Université de Poitiers, France in 2016. His research interest includes numerical analysis and simulations of various flow problems, such as non-Newtonian flows and electrohydrodynamic flows. He is also interested in flow control and reduced-order modelling of complex flows, including machine learning aided flow manipulation.
